4 Chapter 10 Techniques of Integration EXAMPLE 1012 Evaluate Z sin6 xdx Use sin2 x = (1 − cos(2x))/2 to rewrite the function Z sin6 xdx = Z (sin2 x)3 dx = Z (1− cos2x)3 8 dx = 1 8 Z 1−3cos2x3cos2 2x− cos3 2xdx Now we have four integrals to evaluate Z 1dx = x and ZAnswer (1 of 8) Thanks for the A!#int sec^5x dx = tanxsec^3x 3int (sec^2x 1) sec^3x dx# and using the linearity of the integral #int sec^5x dx = tanxsec^3x 3int sec^3x dx 3 int sec^5x dx# The integral now appears on both sides of the equation and we can solve for it obtaining a reduction formula #int sec^5x dx = 1/4(tanxsec^3x 3int sec^3x dx)#
What Is Integral Of Sin2x Tan2x Quora
Tan^2x formula integration
Tan^2x formula integration-V = cos x ∫e x sin(x)dx = e x cos x ∫ e x cos x dx 1 Now, we have to repeat the integration process for ∫ e x cos x dx, which is as follows u = e x;Use Subtitution tan x




Integration Calculus Notes
Math\begin{align} \displaystyle \int \frac{1 \tan^2(x)}{1 \tan^2(x)} \, \mathrm{d}x &= \displaystyle \int \frac{\left(\frac{\cos^2(x) \sin^2(x)}{\cos^2(xHow to find the integral of tan(2x)In this tutorial we go through the steps to find the integral of tangent(2x) using the usubstitution integration methodIntegration by Reduction Formulae Suppose you have to ∫e x sin(x)dx We use integration by parts to obtain the result, only to come across a small snag u = e x;
2x if x is positive and close enough to Gerry Myerson hasn't made his into an answer and some time has passed, and no one else has posted such a simple answer Recursive formula for definite integral Recursive formula for definite integralTo integrate tan^22x, also written as ∫tan 2 2x dx, tan squared 2x, (tan2x)^2, and tan^2(2x), we start by utilising standard trig identities to change the form of the integral Our goal is to have sec 2 2x in the new form because there is a standard integration solution for that in formula booklets that we can use We recall the Pythagorean trig identity, and multiply the angles by 21 Answer1 Active Oldest Votes 2 You can always decide whether an indefinite integral is correct by differentiating the answer to see whether you get back the original function So, differentiate your answer do you get tan 2 x sec
(tan^2x1)dxintdx=tanxxc# Answer link Related questions How do you prove the integral formula #intdx/(sqrt(x^2a^2)) = ln(xsqrt(x^2a^2))Calculus Techniques of Integration Integration by Trigonometric Substitution 2 Answers GióIntegrals of Inverse Trigonometric Functions When studying integrals in calculus, one will eventually come across integrals of inverse trigonometric functions




Answered 1 Vxx 11 Vx 1 4 Verify By Bartleby
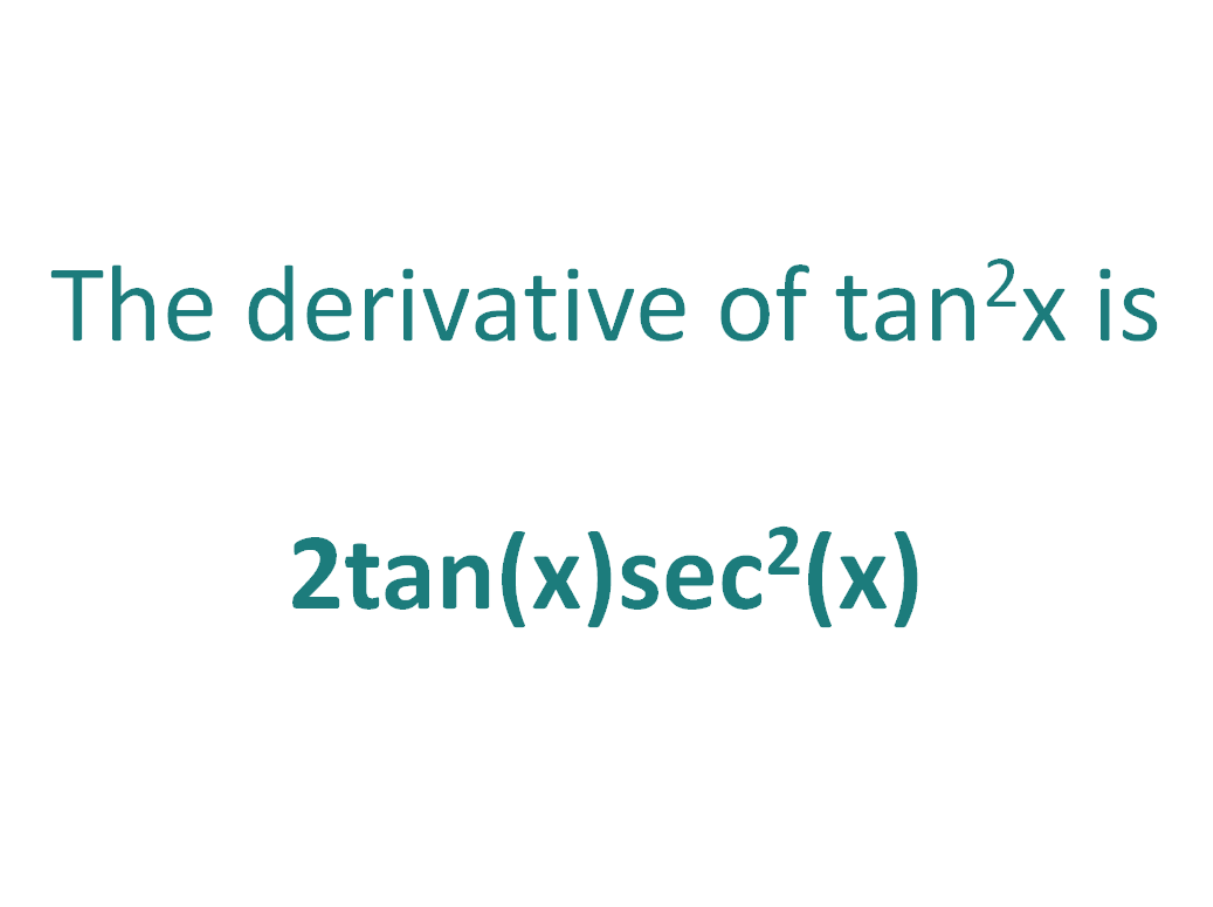



The Derivative Of Tan 2x Derivativeit
Lets use tan 3 as an example Here in an integral calculator when it gets to tan 4 (x) it uses the reduction formula BUT When I ask it to integrate Tan 3 (x) the answer resembles nothing like the reduction formulaTo integrate cot^2x, also written as ∫cot 2 x dx, cot squared x, (cot x)^2, and cot^2(x)we start by using standard trig identities to simplify the integral to a form we can work with We start with this standard and wellknown trig identity for cot 2 x We rearrange the Pythagorean for cos 2 x so that we can substitute it into our previous trig identityWwwmathportalorg 5 Integrals of Trig Functions ∫sin cosxdx x= − ∫cos sinxdx x= − sin sin22 1 2 4 x ∫ xdx x= − cos sin22 1 2 4 x ∫ xdx x= sin cos cos3 31 3 ∫ xdx x x= − cos sin sin3 31 3 ∫ xdx x x= − ln tan sin 2 dx x xdx x ∫=




Solved 2 Evaluate V9 43 Dr For F C Set Up An Integral T0 Compute The 0 1j Then Evaluate The Arc Length Of Y F R For A In The Interval Integral Evaluate Tan 2x




Integration Tan Sec2x 1 Tan2x Dx Mathematics Topperlearning Com Fod22d
Integration Reduction Formulas Any positive integer power of sin x can be integrated by using a reduction formula Example Prove that for any integer n 2, Z sin n xdx= 1 n sin C to find the integrals of tan2 x, tan3 x, tan4 x and tan5 x Using the identity tan2 x =sec2 x 1, Z tan n xdx= Z tan n2 xtan2xdx= Z tan n2 x(sec2x 1) dx = Z tanCos2x Formula, Graph, Integration, Diffrentiation Home Education Cos2x Formula, Identity, Graph, Integration, Diffrentiation Cos2x Formula, Identity, GraphIntegration of Secx Tanx Integration of the secant tangent function is an important integral formula in integral calculus, and this integral belongs to the trigonometric formulae The integration of secant tangent is of the form ∫ sec x tan x d x = sec



bestpictjcry Tan 2x Tan 2x
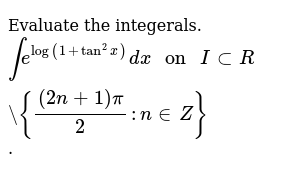



Evaluate The Integerals Br Int E Log 1 Tan 2 X Dx
The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is \(Sin 2x = 2 sin x cos x\) Where x is the angle Source enwikipediaorg Derivation of the FormulaTo integrate tan^2x by parts, also written as ∫tan 2 x dx, tan squared x, and (tan x)^2, we start by using the standard trig identity to adjust the integral for our needs so that we can use the standard parts formula Here is a standard trig identity Since tanx=sinx/cosx, all we have done is multiply both sides to give the above expressionEx 72, 21 tan2 (2𝑥 – 3) Let I = tan2 (2𝑥 – 3) 𝑑𝑥 = sec2 2𝑥 – 3−1 𝑑𝑥 = sec2 2𝑥 – 3 𝑑𝑥− 1𝑑𝑥 =
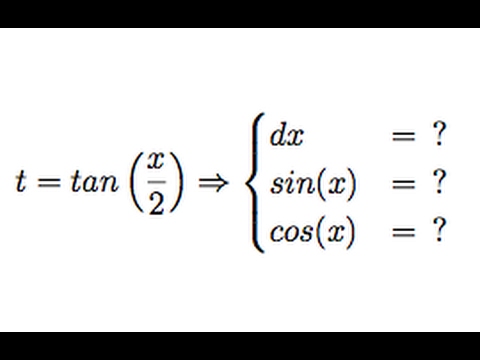



T Tan X 2 Weierstrass Substitution Youtube




Trigonometric Identities Edexcel A Level Maths Pure Revision Notes
Ex 76, 13 Integrate the function tan^(−1) 𝑥 ∫1 〖 tan^(−1) 𝑥 〗 𝑑𝑥=∫1 〖(tan^(−1) 𝑥) 1𝑑𝑥 〗 = tan^(−1) 𝑥∫1Integrate tan2x To integrate tan2x, also written as ∫tan2x dx, and tan 2x, we use the u substitution because the integral of tanu is a standard solution in formula books Let u=2x Then, du/dx=2 We transpose for dx to get the above expression Hence, our new integration can be writtin in terms of u and is simpler to solveChapter 7 Class 12 Integration Formula Sheet by teachoocom Basic Formulae = ^( 1)/( 1) , 1 , = = sin x C = cos x C 2 = tan x c 2 = cot x c = sec x c



What Is The Integration Of Tan 2x Solution Quora
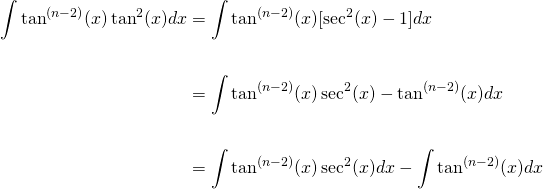



Reduction Formula For The Integral Of Tan N X Dx Steemit
Sin 2x/cos 2x isThe integration of tangent inverse is of the form I = ∫ tan – 1 x d x To solve this integration, it must have at least two functions, however it has only one function tan – 1 x So, consider the second function as 1 Now the integration becomes I = ∫ tan – 1 x ⋅ 1 d x – – – ( i) The first function is tan – 1 x and theIntegral of tan^2x, solution playlist page http//wwwblackpenredpencom/math/Calculushtmltrig integrals, trigonometric integrals, integral of sin(x), integ




Answered Find The Indefinite Integral Sec 2x Bartleby




Tan3x Formula 35 Images Geneseo Math 222 01 Trigonometric Integration Tanx2 Formula Class 11 Maths Sin3x Cos3x Tan3x Formula S
La fórmula de integral de tan es $\displaystyle \int \tan u \cdot du =$ $\ln \sec u$ $= \log \cos u$ De tantas integrales trigonométricas, a continuación veremos unos ejemplos para integrales de tangente Ejemplo 1 Integral de tan 2x $$\int \tan(2x) \ dx=$$1 Answer Active Newest Oldest mathemerize Posted 0 Comments Here, 2 t a n − 1 ( 2 x 1) = c o s − 1 x cos (2 t a n − 1 ( 2 x 1)) = x { We Know cos2x = 1 − t a n 2 x 1 t a n 2 x } ∴ 1 − ( 2 x 1) 2 1 − ( 2 x 1) 2 = x (1 – 2x – 1) (1 2x 1) = x ( 4 x 2 4 x 2) 2x2 (x 1) = 2x ( 2 x 2 2 xTan 2x Formula Tan 2x is an important trigonometric function Tan 2x formula is one of the very commonly used double angle trigonometric formulas and can be expressed in terms of different trigonometric functions such as tan x, cos x, and sin x



What Is The Integral Of Tan X 2 Quora




Tan2x ただの悪魔の画像
Sec 2x is the derivative of tan sec x Is SEC 2x always positive?Integrate tan^2x sec^3x Reduction formula PracticeExampleAnswer (1 of 4) Let x = \tan \theta, so that \theta = \tan^{1} x, dx = \sec^2{\theta} d\theta Then the given integral is equivalent to \displaystyle \int \tan^{1




Tangent Half Angle Formula Wikipedia
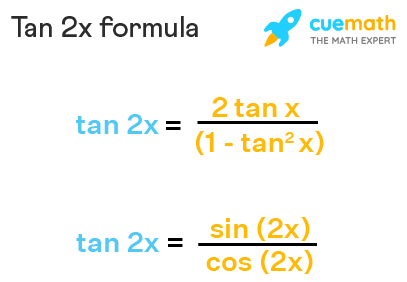



Tan 2x Formula What Is Tan 2x Formula Examples
You get these gems as you gain rep from other members for making good contributions and giving helpful advice nope, the simple way is to rewrite tan2x as sin2x/cos2x then integrate by substitution I get the answer as 1/2 ln (cos2x) cAs there is no way to immediately integrate tan^2(x) using well known trigonometric integrals and derivatives, it seems like a good idea would be writing tan^2(x) as sec^2(x) 1 Now, we can recognise sec^2(x) as the derivative of tan(x) (you can prove this using the quotient rule and the identity sin^2(x) cos^2(x) = 1), while we get x when we integrate 1, so our final answer is tan(x)The reduction formula for tan n x is a confusing matter for me, First how do you derive it?



Tan2x ただの悪魔の画像




Integral Of Sec 2x Tan 2x Integral Example Youtube
So here it is Recall that \tan x <What is the integral of tan1 (2x)?Integral of tan^4(x), calculus, integrationsolution playlist page http//wwwblackpenredpencom/math/Calculushtmltrig integrals, trigonometric integrals, in




Integrate Cosec 2x



3
This is very easy, and this involves the use of trig identities \displaystyle \int \tan ^2\left(x\right)\,dx Since \tan ^2\left(x\right)=1\sec ^2\left(x\right), so we rewrite the equation as \displaystyle \int \tan ^2\left(x\right)=\int 1\sec ^2\leftIntroduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formulaIntegration Formulas Integration is the process of continuous summing and is usually considered as the reverse process of Differentiation Therefore, integrals are also called antiderivatives This means that if d/dxf(x)=g(x) then, ∫g(x)dx=f(x)C Integration formulas are used to find the integrals of algebraic expressions, trigonometric ratios, inverse trigonometric




Tan2x ただの悪魔の画像




Weierstrass Substitution Wikipedia
$$\int sec^2x \tan^2x dx = tan^2x 2\int \sec^2x \tan^2x dx$$ You can move the $ 2\int \sec^2x \tan^2x dx$ to the left hand side of the equation by addition $$\int \sec^2x \tan^2x dx 2\int \sec^2x \tan^2x dx= tan^2x c, c\in\mathbb{R}$$ Note that once we have a side without an integral on it you need to include a constant of integrationDv/dx = cos x86 Integrals of Trigonometric Functions Contemporary Calculus 5 If the exponent of secant is even, factor off sec2(x), replace the other even powers (if any) of secant using sec2(x) = tan2(x) 1, and make the change of variable u = tan(x) (then du = sec2(x) dx ) If the exponent of tangent is odd, factor off sec(x)tan(x), replace the remaining even powers (if any) of



What Is Integral Of Sin2x Tan2x Quora



1
Yes, sec 2x is always positive What is tan 2x equal to?`int((cos^1 2x)^4)/(sqrt14x^2) dx` Put `v = cos^1 2x` (since this is the only substitution that works The other likely one, `v=14x^2`, doesn't give us anything useful when we differentiate while doing the integral I'm using `v` this time, so as not to confuse things with `u` in the following formula) We need to find `(dv)/dx`Trigonometric substitutions are a specific type of u u u substitutions and rely heavily upon techniques developed for those They use the key relations sin 2 x cos 2 x = 1 \sin^2x \cos^2x = 1 sin2 xcos2 x = 1, tan 2 x 1 = sec 2 x \tan^2x 1 = \sec^2x tan2 x 1 = sec2 x, and cot




Weierstrass Substitution Wikipedia




Ex 7 2 21 Integrate Tan2 2x 3 Class 12 Cbse Ex 7 2
Dv/dx = sin x So, du/dx = e x;Get an answer for 'Prove the following reduction formula integrate of (tan^(n)x) dx= (tan^(n1)x)/(n1) integrate of (tan^(n2))dx' and find homework help for other Math questions at eNotesWe obtain the following integral formulas by reversing the formulas for differentiation of trigonometric functions Integrate `int csc 2x\ cot 2x\ dx` Answer `intcsc\ 2x\ cot 2x\ dx `=1/2csc\ 2xK` Integrals of tan x, cot x Now, if we want to find `int tan x\ dx`, we note that `int tan x\ dx=int(sin x)/(cos x)dx` Let `u=cos




Integrate Tan 2x By Parts




Solved Integral 18 Tan 2 X Sec 2 X 2 Tan 3 X 2 Dx Find Chegg Com
Now, the integral of sec x is completed Formula of Sec x The formula of secant of x is 1 divided by the cosine of x sec x = 1 cos x Some frequently asked questions What is the derivative of tan sec x?Dave's Math Tables Integral tan (x) ( Math Calculus Integrals Table Of tan x) Discussion of tan x = lncos x C 1 Proof Strategy Make in terms of sin's and cos's;Reduction formula is regarded as a method of integration Integration by reduction formula helps to solve the powers of elementary functions, polynomials of arbitrary degree, products of transcendental functions and the functions that cannot be integrated easily, thus, easing the process of integration and its problems Formulas for Reduction in Integration




Integral Of Tan 2x Youtube




Integration Calculus Notes
Answer (1 of 3) This is simple \displaystyle \int \tan ^2\left(2x\right)dx Since \tan ^2\left(x\right)=1\sec ^2\left(x\right) \displaystyle =\int \1\sec ^2




Tan 2x Formula What Is Tan 2x Formula Examples




Integrate Sec 2x Method 2




What Is The Integration Of Tan 2x Solution Quora




Integral Of Tan 2x Cot 2x 2 Calculus 1 Trig Integrals Youtube




Integral Of Tan X Video Khan Academy




Integral Of The Secant Function Wikipedia




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Integration Trig Identities Ppt Download
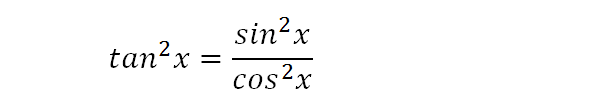



Integrate Tan 2x By Parts
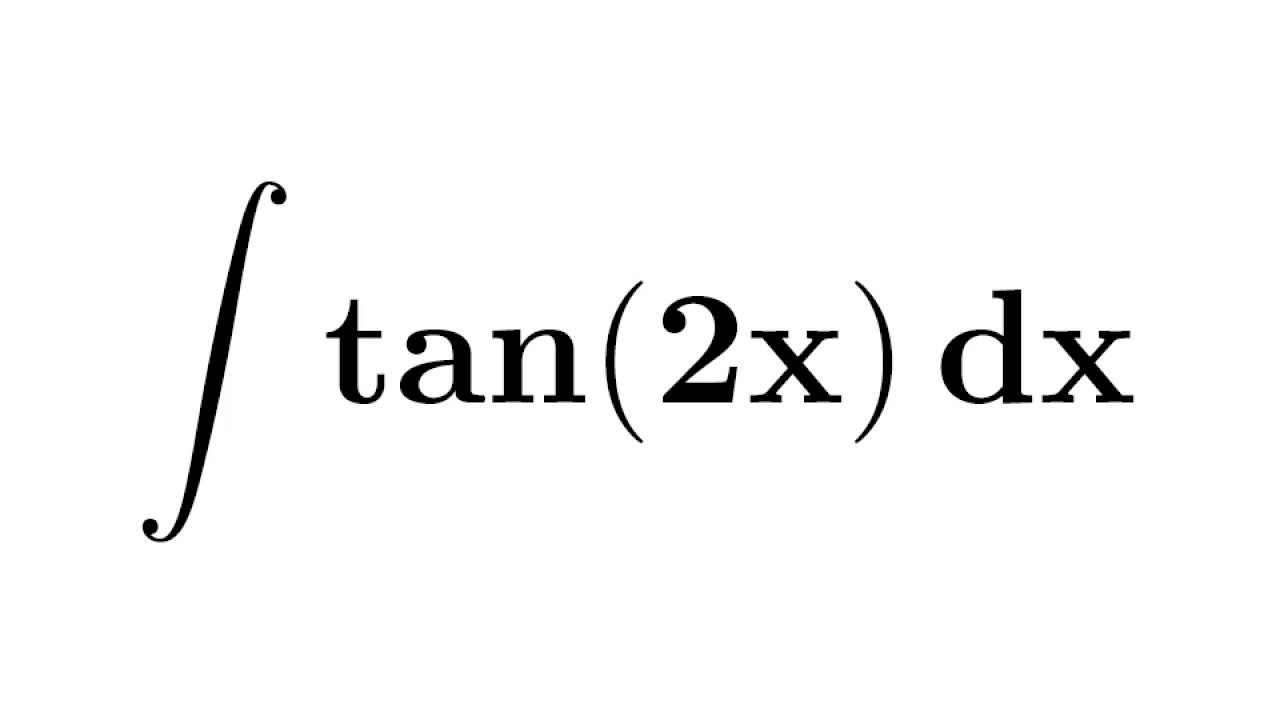



Integral Of Tan2x Integration Of Tan2x Antiderivative Of Tan2x Integral Of Tan 2x Youtube




Integration Trig Identities Ppt Download




Integrate Tan2x




Trigonometric Integrals Geogebra
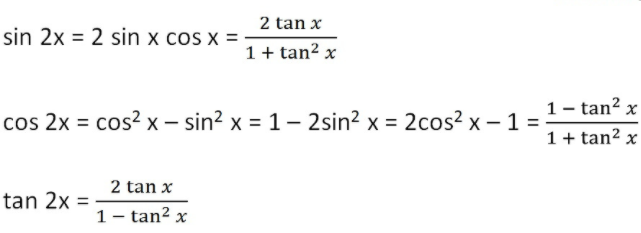



Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec




Integrate Tan2x




Weierstrass Substitution Wikipedia




Power Series Of Arctan 2x Video Khan Academy




Ex 7 4 9 Integrate Sec 2 X Root Tan 2 X 4 Ncert Class 12




Evaluate Inttan X Theta Tan X Theta Tan2x Dx




Integral Of Tan 2 X Youtube




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco




Analytic Trig Ppt Video Online Download




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com




Integration Of Tan 2 X Sec 2 X Youtube




Tan2x Sec2x ただの悪魔の画像




Weierstrass Substitution Wikipedia
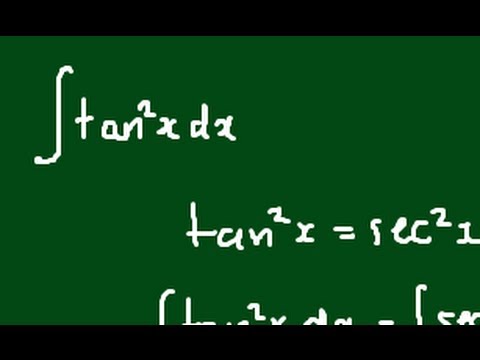



How Do I Integrate Tan 2 X Youtube



What Is The Formula Of Tan2x Quora



2




How Do You Integrate 1 Tan2x Sec2x Dx Socratic




Integration Of Trigonometric Functions



Tan2x 1 ただの悪魔の画像



1



What Is The Formula Of Tan2x Quora




Integration Calculus 2



What Is Math Int Tan 2 2x Dx Math Quora



What Is Integral Of Sin2x Tan2x Quora
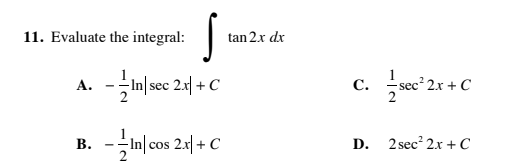



Answered 11 Evaluate The Integral Tan 2x Dx A Bartleby




Ex 7 2 21 Integrate Tan2 2x 3 Class 12 Cbse Ex 7 2




Weierstrass Substitution Wikipedia
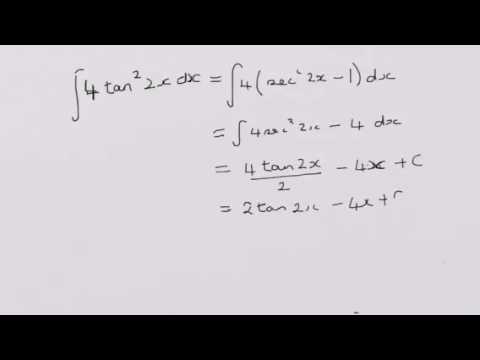



Integrating Tan 2 2x Youtube




Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3
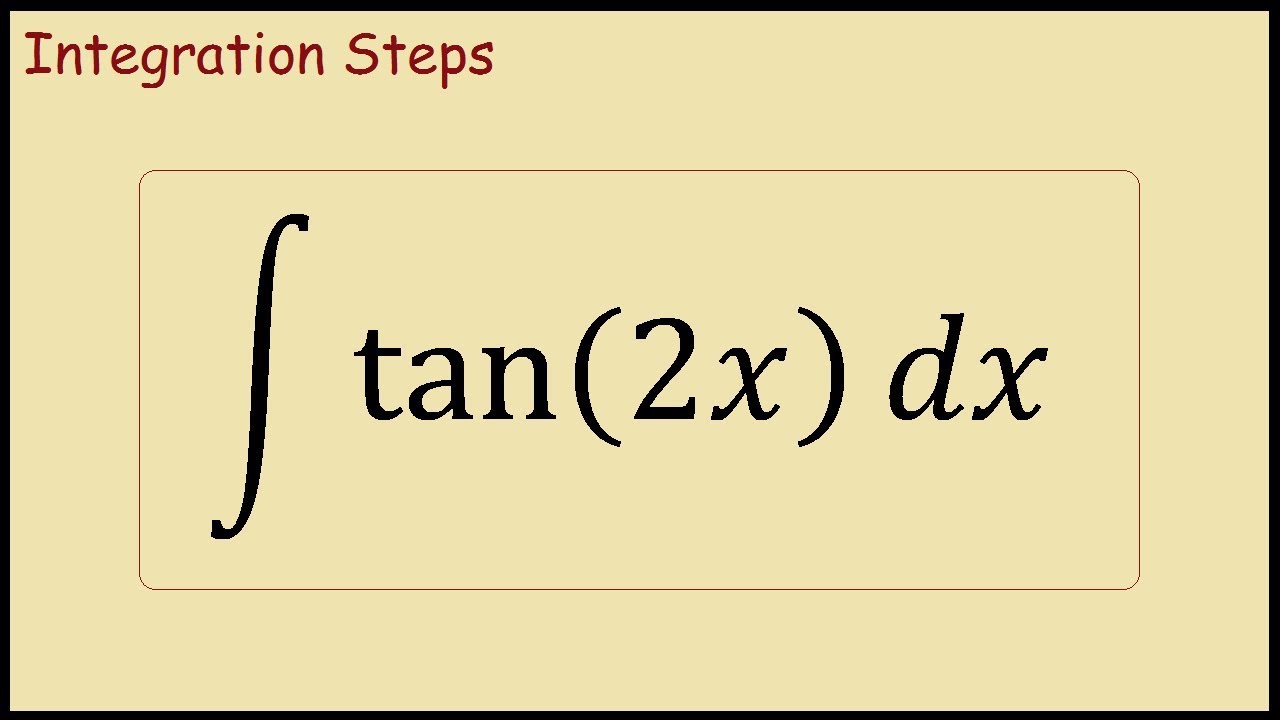



How To Integrate Tan 2x Youtube
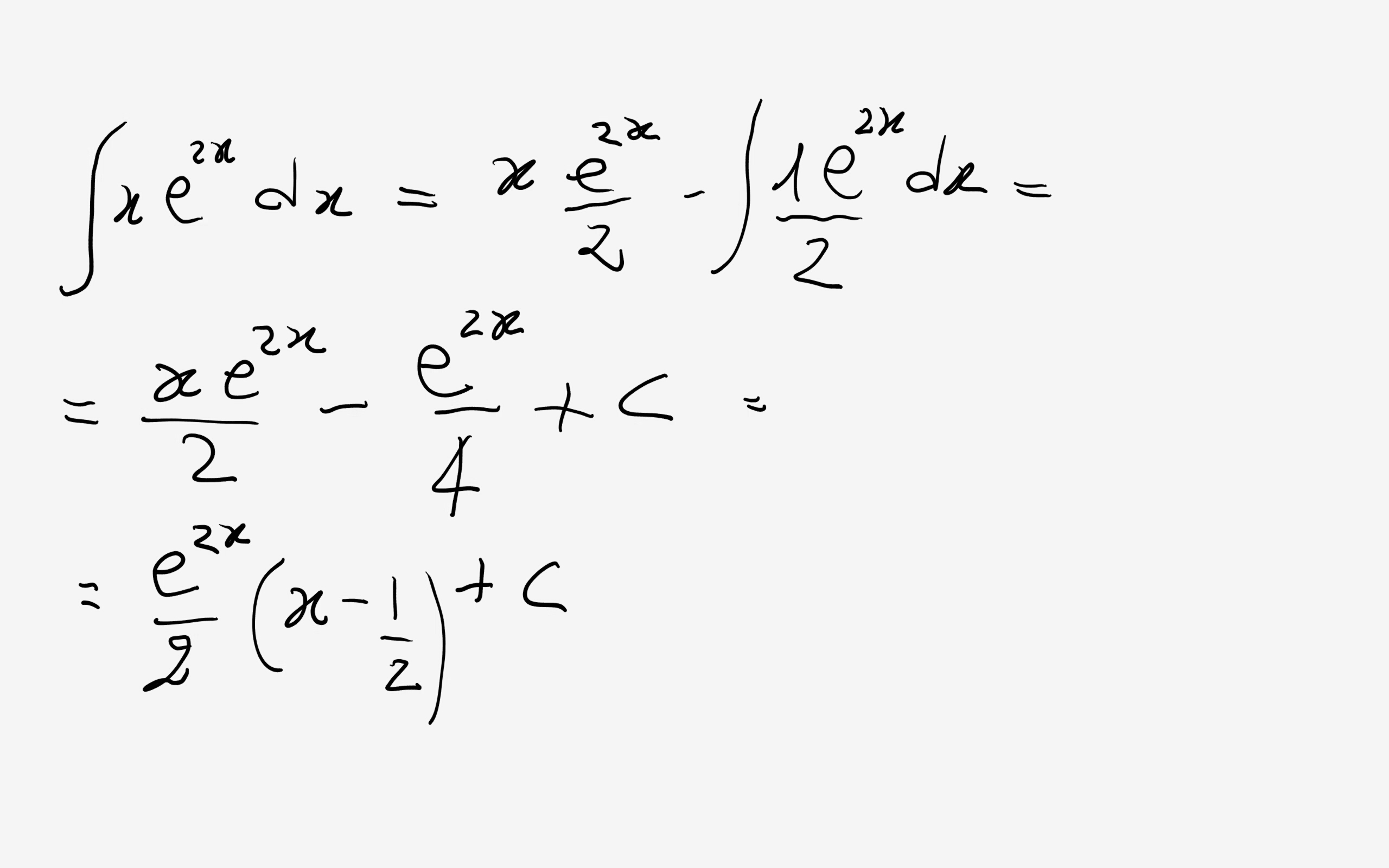



How Do You Integrate Xe 2x Dx Socratic




Integration Tan 1 2x 1 X2 Dx Explain In Great Detail Mathematics Topperlearning Com 6a0lwo11



What Is The Formula Of Tan2x Quora



bestpictjcry Tan 2x Tan 2x




bestpictjcry Tan 2x Tan 2x




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube



Solve By The Method Of Variation Of Parameters D 2y Dx Y Tan2x Sarthaks Econnect Largest Online Education Community



1



Integral Of Sec 6 X Tan 2 X Dx




Cot 2x 35 Images Solve 2 Cot 2x Solved Prove The Identity Cot 2x 1 2x Pink Fylo Cot Bed Fitted Sheet 100 Cotton




Integrate Tan 2x




Tan2x ただの悪魔の画像



Tan2x ただの悪魔の画像




Integrate Tan 2x By Parts
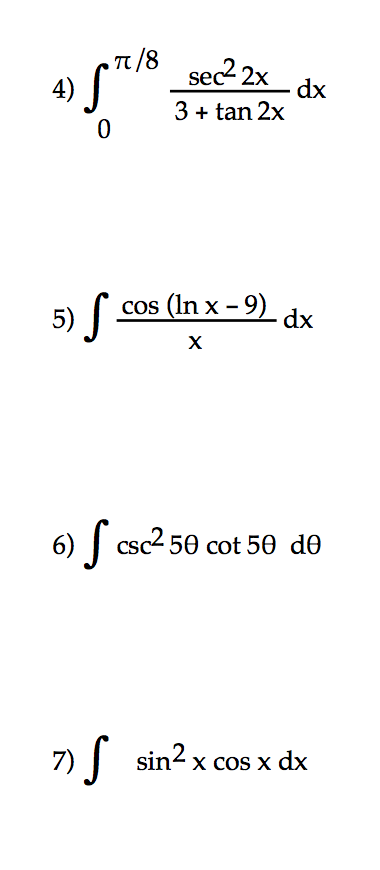



Solved Integral Pi 8 0 Sec 2 2x 3 Tan2x Dx Integral Cos Ln Chegg Com



What Is Math Int Tan 2 2x Dx Math Quora




Integral Of Tan 2x Formula Proof Examples




Weierstrass Substitution Wikipedia




bestpictjcry Tan 2x Tan 2x




Misc 44 Mcq Value Fo Tan 1 2x 1 1 X X2 Dx Is




Integral Of Sec X Formula Proof Integration Of Sec X



What Is The Integration Of Tanx Tan2x Tan3x Dx Quora




Int 1 Tan 2x 1 Tan 2x Dx




1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit
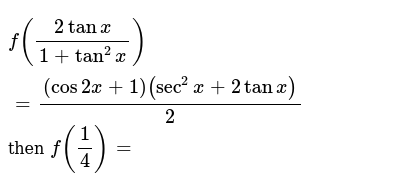



いろいろ Tan2x 1sec2x ただの悪魔の画像




Integration Of Inverse Tan 2x Integration By Parts Youtube




Misc 44 Mcq Value Fo Tan 1 2x 1 1 X X2 Dx Is
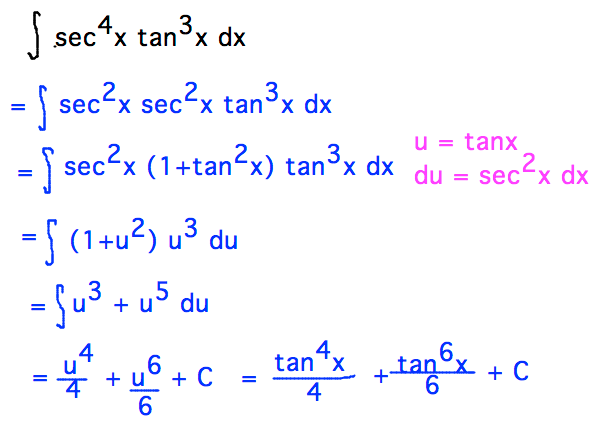



Geneseo Math 222 01 Trigonometric Integration




Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3




Integral Tan 2 X Sec X Youtube



What S The Integral Of Tan 2x Quora



0 件のコメント:
コメントを投稿